Step Generalized Double DEMA (ATR based) [Loxx]

2022년 9월 8일

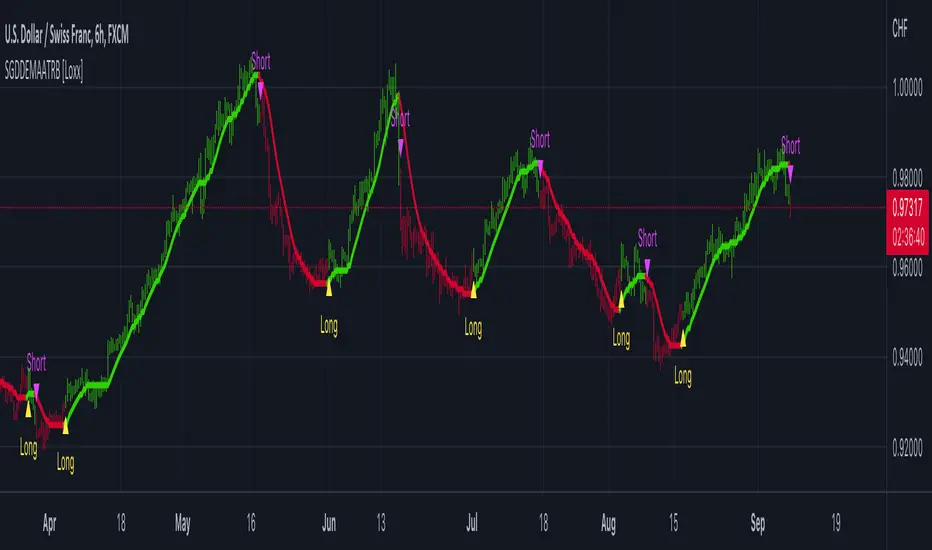
Step Generalized Double DEMA (ATR based) [Loxx] works like a T3 moving average but is less smooth. This is on purpose to catch more signals. The addition of ATR stepped filtering reduces noise while maintaining signal integrity. This one comes via Mr. Tools.

Theory:
The double exponential moving average (DEMA), was developed by Patrick Mulloy in an attempt to reduce the amount of lag time found in traditional moving averages. It was first introduced in the February 1994 issue of the magazine Technical Analysis of Stocks & Commodities in Mulloy's article "Smoothing Data with Faster Moving Averages". The way to calculate is the following :

The Double Exponential Moving Average calculations are based combinations of a single EMA and double EMA into a new EMA:

1. Calculate EMA

2. Calculate Smoothed EMA by applying EMA with the same period to the EMA calculated in the first step

3. Calculate DEMA

DEMA = (2 * EMA) - (Smoothed EMA)

This version:
For our purposes here, we are using Tim Tillson's (the inventor of T3) work, specifically, we are using the GDEMA of GDEMA for calculation (which is the "middle step" of T3 calculation). Since there are no versions showing that "middle step, this version covers that too. The result is smoother than Generalized DEMA, but is less smooth than T3 - one has to do some experimenting in order to find the optimal way to use it, but in any case, since it is "faster" than the T3 (Tim Tillson T3) and still smooth, it looks like a good compromise between speed and smoothness.

Usage:
You can use it as any regular average or you can use the color change of the indicator as a signal.

Included

• Alerts
  
• Signals
  
• Bar coloring
  
• Loxx's Expanded Source Types