Dynamically Adjustable Filter

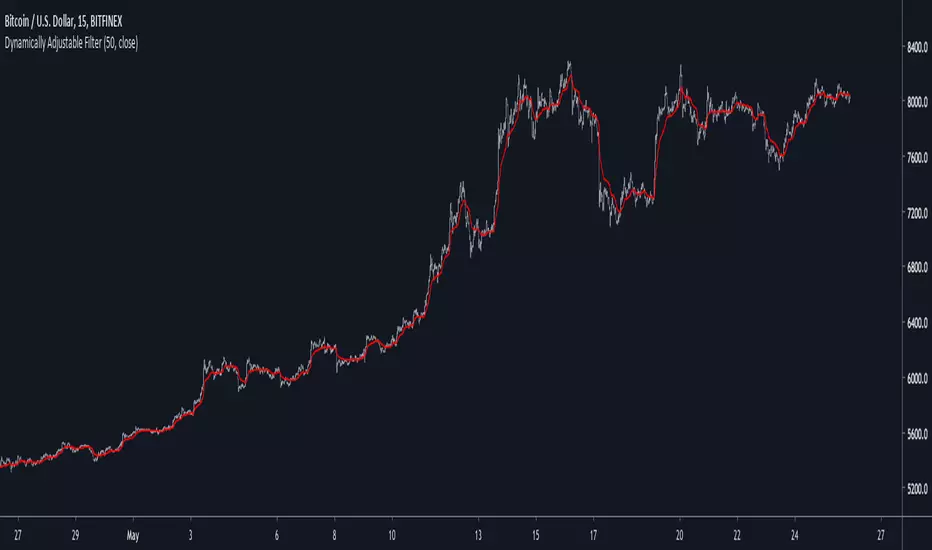
Introduction

Inspired from the Kalman filter this indicator aim to provide a good result in term of smoothness and reactivity while letting the user the option to increase/decrease smoothing.

Optimality And Dynamical Adjustment

This indicator is constructed in the same manner as many adaptive moving averages by using exponential averaging with a smoothing variable, this is described by :

x= x_1 + a(y - x_1)

where y is the input price (measurements) and a is the smoothing variable, with Kalman filters a is often replaced by K or Kalman Gain, this Gain is what adjust the estimate to the measurements. In the indicator K is calculated as follow :

K = Absolute Error of the estimate/(Absolute Error of the estimate + Measurements Dispersion * length)

The error of the estimate is just the absolute difference between the measurements and the estimate, the dispersion is the measurements standard deviation and length is a parameter controlling smoothness. K adjust to price volatility and try to provide a good estimate no matter the size of length. In order to increase reactivity the price input (measurements) has been summed with the estimate error.

Now this indicator use a fraction of what a Kalman filter use for its entire calculation, therefore the covariance update has been discarded as well as the extrapolation part.

About parameters length control the filter smoothness, the lag reduction option create more reactive results.

Conclusion

You can create smoothing variables for any adaptive indicator by using the : a/(a+b) form since this operation always return values between 0 and 1 as long as a and b are positive. Hope it help !

Thanks for reading !

릴리즈 노트:

Updated to version 3