[CS] NWMA Moving Average 3.0

2019년 3월 9일

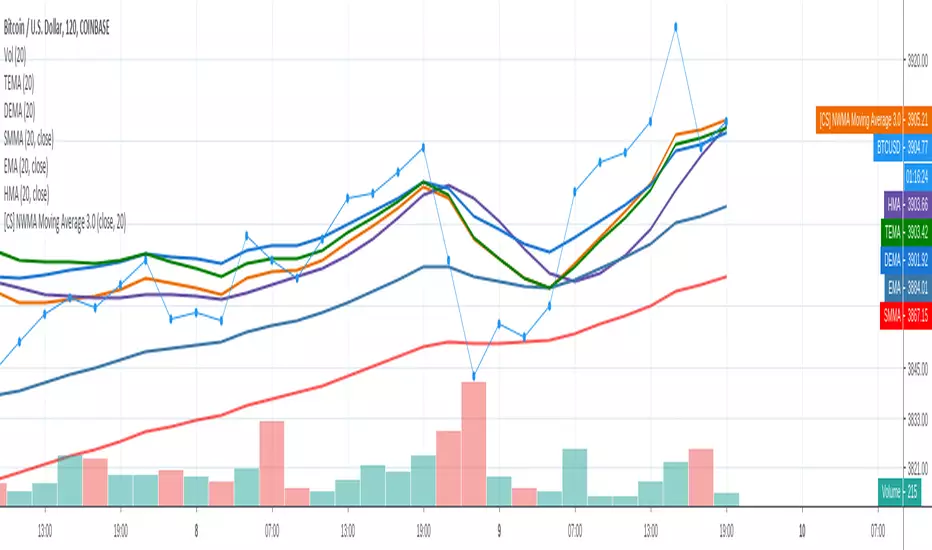
PineScript Implementation of Moving Average 3.0 first referenced by Manfred G. Dürschner as New wma or Nwma.

See amazing original paper Moving Averages 3.0 at page 27:
ifta.org/public/files/journal/d_ifta_journal_12.pdf


As shown in the picture Nwma is performing better than DEMA, TEMA, EMA, and other common used moving averages such as Hull MA that is prone to overshooting. With NWMA lag is extremely reduced.

As already implemented in NinjaTrader C# Nwma plugin by sumana.m:
ninjatrader.com/support/forum/forum/ninjatrader-7/indicator-development-aa/74275-nwma-ifta-2012-mov-avg-3-0


(from the original paper)

Nyquist Criterion
In signal processing theory, the application of a MA to itself can be seen as a Sampling procedure. The sampled signal is the MA (referred to as MA1) and the sampling signal is the MA as well (referred to as MA2). If additional periodic cycles which are not included in the price series are to be avoided sampling must obey the Nyquist Criterion [1, 4]. With the cycle period as parameter, the usual one in Technical Analysis, the Nyquist Criterion reads as follows: n1 = λ*n2 , with λ ≥ 2. n1 is the cycle period of the sampled signal to which a sampling signal with cycle period n2 is applied. n1 must at least be twice as large as n2. In Mulloy´s and Ehlers´ approaches (referred to as Moving Averages 2.0) both cycle periods are equal. Moving Averages 3.0 Using the Nyquist Criterion there is a relation by which the application of a MA to itself can be described more precisely. In figure 2 a price series C (black line), one MA (MA1, red line) with lag L1 to the price series and another MA with lag L2 to MA1 (MA2, blue line) are illustrated. Based on the approximation and the relations described in figure 2 the following equation holds: (1) D1/D2 = (C – MA1)/(MA1 – MA2) = L1/L2 According to the lag formulas in the introduction L1/L2 can be written as follows:

α := L1/L2 = (n1 – 1)/(n2 – 1).

In this expression denominator 2 for the SMA and EMA as well as denominator 3 for the WMA are missing. α is therefore valid for all three MAs.

Using the Nyquist Criterion one gets for α the following result:
(2) α = λ* (n1 – 1)/(n1 – λ).
α put in (1) and C replaced by the approximation term NMA, the notation for the new MA, one gets:
NMA = (1 +α) MA1 – α MA2.
In detail, equation (2) reads as follows:
(3) NMA[price/ n1, n2] = (1 + α) MA1[price/ n1 ] – α
MA2[MA1/ n2],
(4) α = λ* (n1 – 1)/(n1 – λ), with λ ≥ 2.
(3) and (4) are equations for a group of MAs (notation: Moving Averages 3.0). They are independent of the choice of an MA. As the WMA shows the smallest lag (see introduction), it should generally be the first choice for the NMA. n1 = n2 results in the value 1 for α and λ, respectively. Then equation (3) passes into Ehlers´ formula. Thus Ehlers´ formula is included in the NMA formula as limiting value. It follows from a short calculation that the lag for NMA results in a theoretical value zero.

Please enjoy,

CryptoStatistical