Bitcoin Logarithmic Fractal Growth Model By ARUDD

2021년 9월 11일

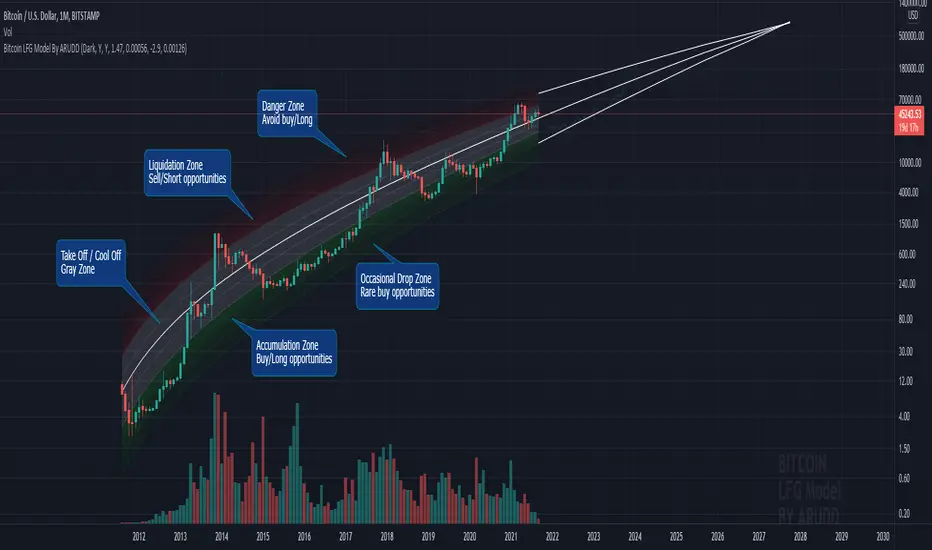
This model, which I'm calling the Logarithmic Fractal Growth Mode (L.F.G), uses Bitcoin's mathematical monetary policy to evaluate the future possible price valuation.

It takes into account fractal (and logarithmic) growth as well as how those who hold bitcoins might react to certain events such as changes in supply and demand. It also shows that it is mathematically logical that someday it must become stable.

The information gained from knowing this helps people make more informed decisions when buying bitcoin and thinking of its future possibilities.

The model can serve as some type of general guideline for determining how much bitcoins should be worth in the future if it follows a certain path from its current price.

Modeling Bitcoin's money supply mathematically, and knowing that there is a finite number of them, makes this whole process much more rational than just thinking about the possibilities in pure subjective terms.

Before going any further I want to say that no one can know with absolute certainty what will happen to bitcoins price in the future, but using mathematics gives us an idea of where things are headed.

The results presented here are based on very reasonable assumptions for how bitcoin might continue to grow (and then level out) once there are over 21 million bitcoins in existence.

The model shows that bitcoin's price can never go down to zero (thus creating the "death spiral" phenomenon), and as such, bitcoin has an extremely high probability of becoming stable as it approaches infinity.

Conversely, this model also shows that at some point there is a high probability that bitcoin will not continue to grow exponentially forever.

Credit goes to Quantadelic for the awesome original script.

ARUDD