Variable Purchase Options [Loxx]

2022년 10월 5일

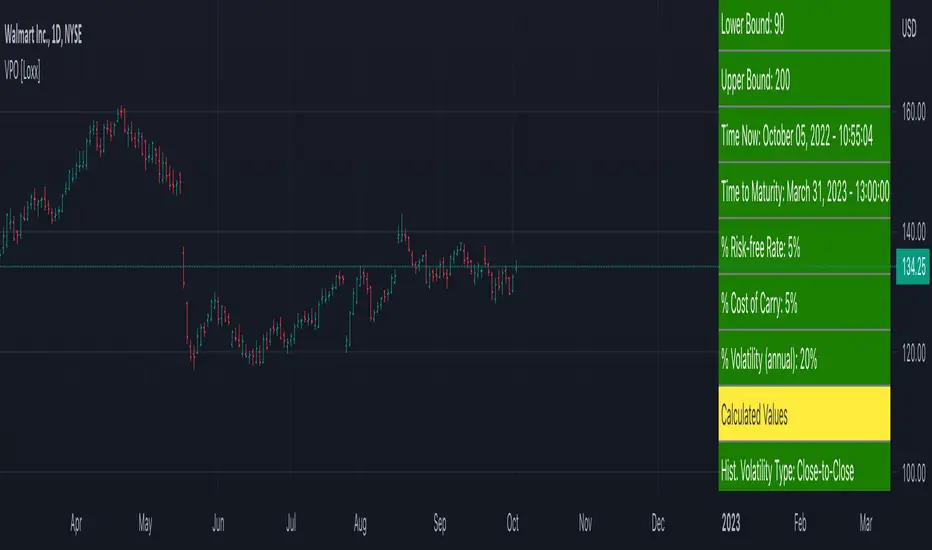
Handley (2001) describes how to value variable purchase options (VPO). A VPO is basically a call option, but where the number of underlying shares is stochastic rather than fixed, or more precisely, a deterministic function of the asset price. The strike price of a VPO is typically a fixed discount to the underlying share price at maturity. The payoff at maturity is equal to max[N x S — X], where N is the number of shares. VPOs may be an interesting tool for firms that need to raise capital relatively far into the future at a given time. The number of underlying shares N is decided on at maturity and is equal to

N = X / St(1 -D)

where X is the strike price, ST is the asset price at maturity, and D is the fixed discount expressed as a proportion 0 > D < 1. The number of shares is in this way a deterministic function of the asset price. Further, the number of shares is often subjected to a minimum and maximum. In this case, we will limit the minimum number of shares to Nmin = X / U(1 -D) if, the asset price at maturity is above a predefined level U at maturity. Similarly, we will reach the maximum number of shares A T = x if the stock price at maturity is equal Nmax = X / L(1 -D) or lower than a predefined level L. Based on Handley (2001), we get the following closed-form solution: (via "The Complete Guide to Option Pricing Formulas")

c = XD / 1-D e^-rT + Nmin(Se^(b-r)T * N(d1) - Ue^-rT * N(d2))
- Nmax(Le^-rT * N(-d4) - Se^(b-r)T * N(-d3))
+ Nmax(L(1-D)e^-rT * N(-d6) - Se^(b-r)T * N(-d5))

where

d1 = (log(S/U) + (b+v^2/2)T) / vT^0.5 ... d2 = d1 - vT^0.5

d3 = (log(S/L) + (b+v^2/2)T) / vT^0.5 ... d4 = d3 - vT^0.5

d5 = (log(S/L(1-D)) + (b+v^2/2)T) / vT^0.5 ... d6 = d5 - vT^0.5

Inputs
Asset price (S)
Strike price (K)
Discount %
Lower bound
Upper bound
Time to maturity
Risk-free rate (r) %
Cost of carry (b) %
Volatility (v) %

Things to know

• Only works on the daily timeframe and for the current source price.
  
• You can adjust the text size to fit the screen
  

2022년 10월 5일

릴리즈 노트

UI updates.