ZM: Cross-Cycle Knot in Triangle

8월 3일

🏛️ Research Notes

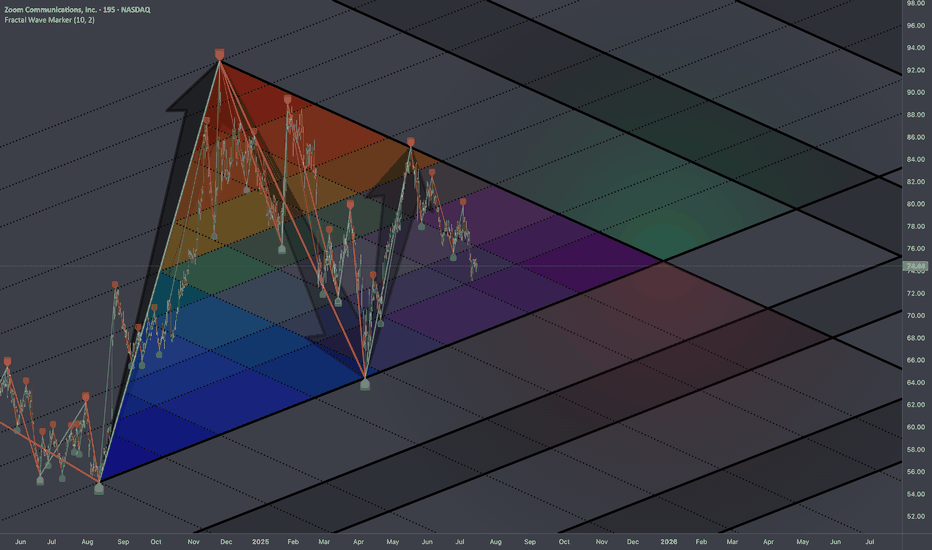
Original

• Alternative Interconnection Experimenting with cross-cycle interconnection so coordinates of the 3 point of fib channels are placed on structure's latest connecting point while abiding its original angles.
• When elements are extended we have a projection that looks like this:
• Other aspects of the shape are being tested
  Fibonacci Channels based on angle of the trend fragments the cycle creating probabilistic levels. (The steeper the angle of the FC the more it relates to time axis.)

8월 3일

노트

Here is how it would have looked if 3rd point of fib channel was based on 1st wave (largest in given illustration).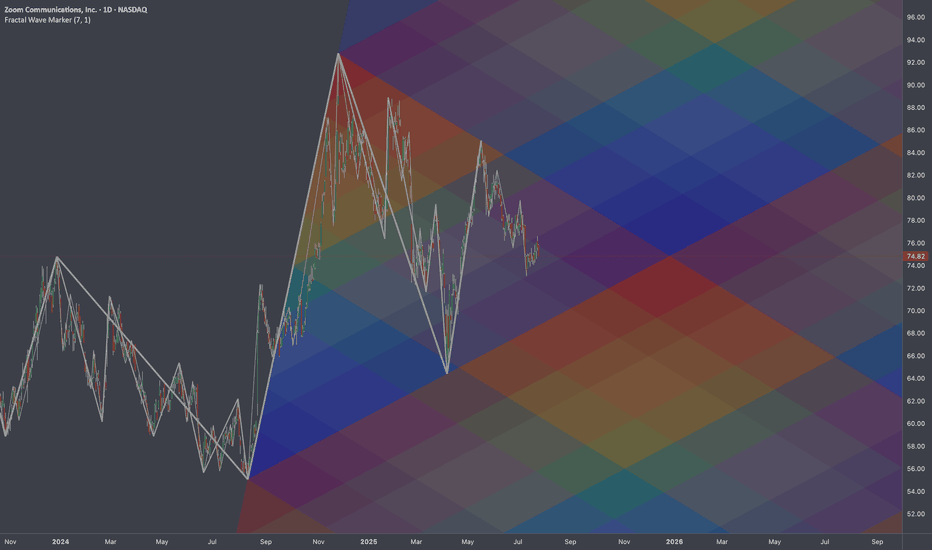

However, with given spectrum of colors that describes transition we actually want 2nd wave as basis as in the main updated chart, because mapping using cross-cycle approach is more tied to chronological order than the way of covering triangle patterns.

8월 8일

액티브 트레이드

Crossing above the curve would serve as confirmation of the triangle pattern.