Jurik RSX on JMA is identical to indicator RSI RSX, except that price data is pre-smoothed by JMA. Doing so extends the range of RSX and produces fewer micro reversals. That lends itself to advanced analysis. Output Range: -100 to +100. What is RSX? RSI is a very popular technical indicator, because it takes into consideration market speed, direction and...
This is a useful indicator which allows you to plot multiple fully customized Moving Averages. Here are some of its features: Ability to fine-tune a wide variety of moving averages: smoothing type, periods, offsets, timeframes, sources, thickness, line/label color and text color. Descriptive labels to avoid misreading. Simple and well-organized Input Tab.
Strategy Introduction This multi-timeframe strategy generates buy and sell entries based on two Moving Averages’ cross with an option to turn on trend direction confirmation through 3rd Moving Average selection. While all three moving averages can be selected from the following list: SMA EMA DEMA TEMA LRC WMA MF VAMA TMA HMA JMA Kijun v2 EDSMA ...
Library "TypeMovingAverages" This library function returns a moving average. ma_fast ma_slow MA_selector() Example // This source code is subject to the terms of the Mozilla Public License 2.0 at mozilla.org // © hapharmonic //@version=5 indicator("Test MATYPE", overlay=true) import hapharmonic/TypeMovingAverages/1 as MAType xprd1 =...
//Sup TV. This script is inspired by (and dedicated to) closure of sales (today, Oct 20 '21) of the famous Jurik Research. ... Jurik Research, the real people who been doing real things by using the real instruments, while many others been reading books "How to become a billionaire in 2 days", watching 5687 hours videos of how to use RSI, and studying+applying...
I want to give credits to @QuantNomad, i got the heikin ashi part of the script from this open script /0iKy7lyG-QuantNomad-Heikin-Ashi-PSAR-Strategy/; and to the other guy that provided a 17 type of moving average script open source but i forgot his name, if someone remember please tell me. My idea was to see how the different types of moving averages behaves in...
MA+ is a multi time frame moving average indicator with more than a dozen different moving averages (like KAMA, VAMA, JMA, HMA and much more). More moving averages will be added on every update, hence Follow me to get notified. MA+ Supports automatic (AUTO in settings) time frame multiplier. For example, if you set 'Auto Resolution Multiplier' to 6, and your...
The Jsa Moving Average was created by George R. Arrington, Ph .D. (Stocks & Commodities V. 11:10 (427-431)) and it is an extremely simple formula but has very many great uses. For one thing it acts as support and resistance levels and it also acts like a trailing stop. It gives a wide enough berth during extended up or down trends to let you ride the wave up or...
This script is designed for the NNFX Method, so it is recommended for Daily charts only. Tried to implement a few VP NNFX Rules This script has a SSL / Baseline (you can choose between the SSL or MA), a secondary SSL for continiuation trades and a third SSL for exit trades. Alerts added for Baseline entries, SSL2 continuations, Exits. Baseline has a Keltner...
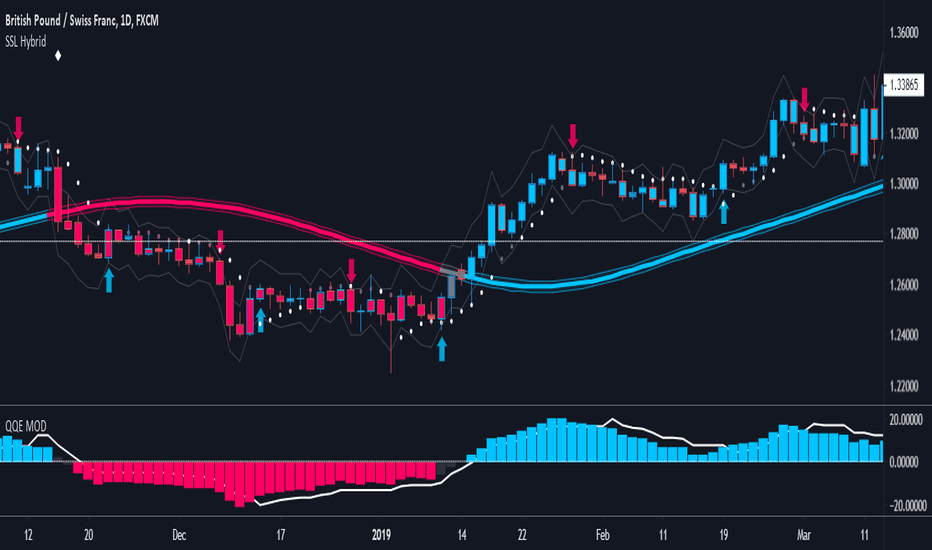
The "AC-P" version of jiehonglim's NNFX Baseline script is my personal customized version of the NNFX Baseline concept as part of the NNFX Algorithm stack/structure for 1D Trend Trading for Forex. Everget's JMA implementation is used for the baseline smoothing method, with optional ATR bands at 1.0x and 1.5x from the baseline. NNFX = No Nonsense Forex ...
This is an old compilation of mine suitable for scalping. To filter out the generated signals use Difference value between on the Settings menu.
This is a PS4 update to my previous 4 JMA strategy that received many likes. In this and several recent strategies I use a simplified strategy setup, featuring trailing stops with very tiny increments. This is done intentionally in order to boost performance to the limit, so that to pinpoint that limit. Strategies with performance of about 90% or above are...
This script allows you to add two moving averages to a chart, where the type of moving average can be chosen from a collection of 15 different moving average algorithms. Each moving average can also have different lengths and crossovers/unders can be displayed and alerted on. The supported moving average types are: Simple Moving Average ( SMA ) Exponential...
Clamped EHMA Oscillator Prototype with 21/200 EHMA with additional JMA smoothing (Credit: @everget) Note: This is an experiment - this is not a polished indicator
Implementation of the "Dickinson Moving Average" from the r/algotrading post by Nathan Dickinson Quoted from the author of the Dickinson Moving Average: "I was experimenting with the “zero lag” code from John Ehlers and the Hull Moving Average and noticed that they seemed to respond in complementary ways when properly set up. With the right starting values,...
Introduction The last indicators i posted where about estimating the least squares moving average, the task of estimating a filter is a funny one because its always a challenge and it require to be really creative. After the last publication of the 1LC-LSMA , who estimate the lsma with 1 line of code and only 3 functions i felt like i could maybe make something...
This indicator was originally developed by Mark Jurik. NOTE: If Mr. Jurik ask me to remove this indicator from public access then I will do it.
![Jurik RSX on JMA [Loxx] USDCAD: Jurik RSX on JMA [Loxx]](https://s3.tradingview.com/0/0RC0Yw8v_mid.png)













![Jsa Moving Average [CC] AAPL: Jsa Moving Average [CC]](https://s3.tradingview.com/u/uv7U7kpS_mid.png)


![Baseline-C [ID: AC-P] AUDJPY: Baseline-C [ID: AC-P]](https://s3.tradingview.com/u/uem3oQo3_mid.png)













